Nichtlineare Regression wird dazu verwendet, ein Modell, das einen funktionalen Zusammenhang
zwischen einer unabhängigen Variable X und einer abhängigen Variable Y beschreibt, an gegebene
Daten anzupassen.
Schritt 1: Auswahl des Modells
Hat man sich für eine nichtlineare Regression als Analysemethode entschieden, so benötigt man ein
Modell, das an die Daten angepasst werden soll. Als Beispiel betrachten wir Daten über den Zerfall
eines radioaktiven Isotops:
Die unabhängige X-Variable beschreibt die Zeit in Sekunden, die Y-Variable entspricht dem
experimentell gemessenen prozentualen Anteil zum Zeitpunkt X noch nicht zerfallener Isotope. Nun
ist aus der Physik bekannt, dass der Zerfallsprozess durch ein exponentielles Zerfallsmodell
beschrieben wird, das wir als mathematisches Modell auswählen.
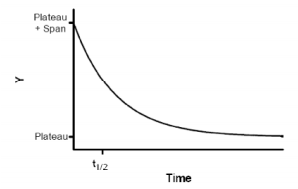
Die zugehörige Formel hat die folgende Gestalt:
Y = Span ⋅ exp (− K ⋅ X ) + Plateau
Das Modell stellt in allgemeiner Form einen funktionellen Zusammenhang zwischen einer
unabhängigen Variable X (z.B. Zeit) und einer abhängigen Variable Y (z.B. Anteil nicht-zerfallener
Isotope) dar.
Zusätzlich enthält jedes Modell Parameter, in unserem Beispiel sind dies:
Parameter:
Plateau – untere Schranke des Zerfalls
Span – Span + Plateau ist Ausgangswert zur Zeit t = 0
K – Rate des Zerfalls (in 1/Zeit)


Das „Anpassen eines Modells“ bedeutet nun genauer, unter allen zugelassen Werten für die
Parameter im Modell diejenige Wahl zu treffen, die die gemessenen Daten „am besten“ erklärt. Die
Standardmethode zur Auswahl dieses Modells ist die Minimierung der Abweichungsquadrate („least
squares method“).
Wie findet man das richtige Modell?
Bevor man eine Regressionsanalyse startet, muss man sich für ein Modell entscheiden. Sollte dies
als eine schwierige Aufgabe erscheinen, scheint es verlockend, die Auswahl des Modells einem
Computerprogramm (z.B. TableCurve von SYSTAT) zu überlassen. Vor diesem Vorgehen sei
ausdrücklich gewarnt. Nimmt man beispielsweise nur die Klasse der Polynomfunktionen, so wird
man in der Regel eine Funktion finden, die hinreichend gut die gemessenen Daten vorhersagt, wenn
man den Grad des Polynoms groß genug wählt. Jedoch wird die Interpretation des Parameters der
angepassten Polynomfunktion nur in den seltensten Fällen gelingen! Daher ist das Modell für eine
wissenschaftliche Auswertung nicht zu gebrauchen. Genau dieses Problem stellt sich auch bei der
automatisierten Auswahl eines Modells durch einen Computer. Dieser hat keinerlei Kenntnisse über
den wissenschaftlichen Hintergrund des zugrunde liegenden Experiments und kann diesen daher
bei der Modellauswahl nicht berücksichtigen. Dies ist jedoch Voraussetzung für die
Interpretierbarkeit der Parameter des Modells. Zusammengefasst bedeutet dies: die Modellauswahl
ist keine mathematische oder statistische Aufgabe, sondern eine wissenschaftliche. Möchte man
eine physikalischen, chemischen oder biologischen Zusammenhang erklären, muss die
Modellauswahl von Wissenschaftlern mit dem entsprechenden Expertenwissen getroffen werden.
Nach der Durchführung der Regressionsanalyse besteht die Möglichkeit, die Güte der
Modellanpassung zu bewerten und ggf. ein erweitertes oder anderes Modell anzupassen.
Schritt 2: Auswahl der anzupassenden Parameter, Nebenbedingungen
Hat man ein Modell ausgewählt, so muss man entscheiden, welche Parameter an die Daten
angepasst werden sollen, in welchem Bereich diese variieren dürfen und welche Parameter vor der
Anpassung auf einen festen Wert gesetzt werden. Betrachten wir erneut das Modell für den
radioaktiven Zerfall,
Y = Span ⋅ exp (− K ⋅ X ) + Plateau
so ist bekannt, dass im Grenzwert großer Zeit alle radioaktiven Isotope zerfallen sind. Daher ist es
geboten, in diesem Fall den Parameter Plateau = 0 zu setzen und nicht durch die Regression
anzupassen. Da es sich um einen abfallenden Zerfallsprozess handelt, ist ebenfalls die
Nebenbedingung K > 0 sinnvoll, da für negative K ein Wachstumsprozess dargestellt wird.
Schritt 3: Auswahl der Startwerte
Nichtlineare Regression ist ein iterativer Prozess. Daher ist es erforderlich, den anzupassenden
Parametern Startwerte zuzuordnen. Dies kann von großer Bedeutung sein, da bei falsch gesetzten
Startwerten der Iterationsprozess u.U. nicht konvergiert. Hat man Startwerte ausgewählt, empfiehlt
es sich, das Anfangsmodell über die gegebenen Daten zu zeichnen, um zu überprüfen, dass das
Startmodell zumindest grob an die Daten angepasst ist.
Schritt 4: Ausführung der Analyse und Interpretation der Ergebnisse
Hat man die nichtlineare Regression ausgeführt, so sind folgende Dinge zu beachten:
• Beschreibt das angepasste Modell die Daten gut?
Zur Beantwortung dieser Frage genügt gelegentlich ein Blick auf den Graphen der Funktion
und die Daten. Hat man z.B. das falsche Modell gewählt, kann es vorkommen, dass der
Konvergenzpunkt der Modellparameter wenig mit den Daten zu tun hat. Ähnliches kann bei
falscher Wahl der Anfangsparameter geschehen. Schließlich gibt es statistische Tests, um
die Güte der Anpassung zu bewerten.
• Sind die angepassten Parameter plausibel?
Der Computer, der die Anpassung durchführt, hat keine Kenntnis der wissenschaftlichen
Bedeutung der Parameter. Daher ist als erstes zu überprüfen, ob die berechneten Parameter
plausibel im Sinne einer wissenschaftlichen Interpretierbarkeit sind. Kommt z.B. in der
Anpassung des radioaktiven Zerfalls ein Parameter Span < 0 heraus, so kann dies zwar
statistisch die beste Anpassung ergeben, physikalisch ergibt sich jedoch kein Sinn, da Span
die Anzahl nichtzerfallener Isotope zum Zeitpunkt t = 0 darstellt. Liegt ein solches
wissenschaftlich unsinniges Resultat vor, so ist das Regressionsergebnis zu verwerfen.
Eventuell kann man durch eine zusätzliche Nebenbedingung und eine erneute Analyse zu
einem sinnvollen Ergebnis gelangen.
• Wie präzise sind die Parameter?
Wie bei jedem statistischen Punktschätzer sind auch bei den berechneten Werten der
nichtlinearen Regression die zugehörigen Konfidenzintervalle von größter Bedeutung. In der
Regel werden neben den Schätzern für die Parameter auch ihr Standardfehler
(Standardabweichung des Punktschätzers) und das 95%-Konfidenzintervall angegeben. Ist
dieses verhältnismäßig klein, liegt eine relativ sichere Schätzung vor, andernfalls ist die
Schätzung mit großer Vorsicht zu betrachten.
Schritt 5: Überprüfung der Voraussetzungen
Jede Regressionsanalyse basiert auf bestimmten Voraussetzungen. Daher ist zu überprüfen, ob
diese erfüllt sind:
• X ist deterministisch, die Variation liegt vollständig in Y.
• Die Streuung in Y folgt für festes X einer bekannten (meist Normal-)Verteilung.
• Die Streuung in Y ist unabhängig von X gleich groß.
• Die Beobachtungen sind unabhängig.
