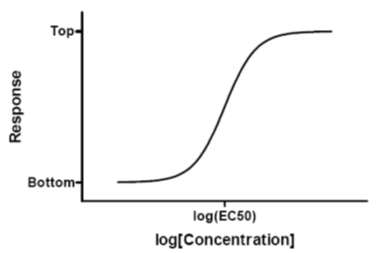
Dosis-Antwort-Sigmoidfunktion (Sigmoidal Dose-Response)
Formel: Y = Bottom + (Top − Bottom) / 1 + 10 log( EC 50) − X
Parameter:
Top – maximale Wirkung
Bottom – Wirkung bei Dosierung 0 (bzw. <<)
log EC 501 / 2 – Logarithmus des EC50 (Wendestelle


Allgemeines, Agonist, Antagonist
Dose-Response-Kurven können als Modelle für viele verschiedene Experimente genutzt werden. Typischerweise bezeichnet X die Konzentration des Medikaments oder des Hormons und Y die untersuchte biologische Antwortvariable, z.B. die Enzymaktivität, das Membranpotential oder die
Kontraktion eines Muskels. Der Begriff „Dose“ (Dosis) wird dabei relativ breit interpretiert, nicht nur im engen Sinne eines Medikaments, das einem Menschen oder Tier in verschiedenen Konzentrationen verabreicht wird. Genauso wird er für In-vitro-Experimente, gelegentlich sogar für
X-Variablen wie Temperatur oder Spannung verwendet. Ein Agonist ist eine Substanz, das an eine Rezeptor bindet und eine Reaktion verursacht. Ist diese Reaktion eine Stimulation in Abhängigkeit der Dosierung, so wird die Dose-Response-Kurve von einem niedrigen Niveau bei kleinen Konzentrationen bergauf zu einem hohen Niveau bei höheren Konzentrationen verlaufen. Verursacht der Agonist eine hemmende (inhibitory) Reaktion, so verläuft die Dose-Response-Kurve umgekehrt von einem hohen Niveau auf ein niedriges Niveau für hohe
Konzentrationen.
Ein Antagonist verursacht selbst keine Reaktion, sondern blockiert eine Agonist-gesteuerte Reaktion. Variiert man daher die Konzentration eines Antagonisten (bei konstanten Konzentration eines zugehörigen Agonisten), so wird die Dose-Response-Kurve genau den umgekehrten Verlauf
der zugehörigen Kurve des Agonisten beschreiben. Die obige Funktion beschreibt allgemein einen Zusammenhang zwischen einer Konzentration einer Substanz oder Enzyms und der zugehörigen Antwort, z.B. einer Wirkung. Sie wird auch als logistische Funktion mit 3 Parametern bezeichnet. Diese verläuft S-förmig von einem niedrigen Niveau (Bottom) auf ein hohes Niveau maximaler Wirkung (Top).
Warum eine logarithmische X-Skala?
Üblich ist eine logarithmische X-Skala, da die Agonisten-Konzentration typischer Weise mehrere Größenordnungen umfasst. Daher ist die graphische Darstellung mit Hilfe einer logarithmischen Skala erheblich einfacher. Die Konzentration wird oft um einen konstanten Faktor erhöht. Dies führt
auf der logarithmischen Skala zu äquidistanten Punkten. Schließlich ist der Fehler des EC50Schätzer auf einer linearen Skala nicht normalverteilt, eine Voraussetzung für viele Analysen. Skaliert man X nicht logarithmisch sondern linear, so entsteht als Antwort-Kurve gerade eine
einfache Bindungsfunktion (One-Site-Binding) wie unter 3.1.
EC50, ED50, IC50
Bei S-förmigen Kurven gibt es genau einen X-Wert, bei dem das mittlere Niveau zwischen Bottom und Top erreicht wird. Dieser Punkt wird als EC50 („effective concentration 50%“) bzw. als ED50 („effective dose 50%“) oder bei fallendem Verlauf als IC50 („inhibitory concentration 50%“)
bezeichnet. In den Formeln wird das Symbol logEC50 verwendet, um daran zu erinnern, dass die XAchse logarithmisch skaliert wird.
Nach Definition hängt der EC50 vom Bottom und Top-Niveau ab. Er ist einer von 4 Parametern, welche die Lage der Dose-Response-Kurve festlegen. Daher wird der EC50 oft als Maß für die Stärke (potency) eines Agonisten verwendet. Man beachte jedoch, dass der EC50 nicht direkt in
Verbindung steht mit der Dissoziationskonstante K d , also kein direktes Maß für die Affinität des Liganden-Rezeptor-Paares ist.
Ein alternatives Maß für die Stärke des Agonisten ist der pEC50, der negative 10-Logarithmus des EC50.
pEC 50 := −log( EC 50)
Oft ist der pEC50 bequemer handhabbar, da der EC50 in Nano- oder Mikromol gemessen wird. Ist z.B. EC50 = 167 nM, so ist pEC50 = 6.78
Steigung – konstant oder variabel?
Bei dieser Dose-Response-Kurve ist das Steigungsverhalten festgelegt. Charakteristisch ist, dass
für den Anstieg von 10% über Bottom auf 90% nicht ganz zwei logarithmische Einheiten auf der X-Achse (genauer: Faktor 81) benötigt werden. Ist diese Voraussetzung nicht gegeben, so muss ein
zusätzlicher Parameter in das Modell eingebracht werden.
